Why are black holes stable against their own gravity?

Neutron stars are timelike matter with a maximum mass of about 2.34 solar masses in quantum chromodynamics (the strong color force). Black holes are spacelike matter that have no maximum mass, but a minimum mass of 2.35 solar masses. Indeed, black holes have been identified with millions or billions of solar masses.

All timelike matter is causal, while black hole spacelike matter is acausal. Acausal spacelike matter has no identifiable particle states (everything is off mass-shell in the spacelike region), no Pauli principle, no equations of motion, no equation of hydrostatic stability, no equations of state, no entropy, no temperature, no Planck constant, no Boltzmann constant, no finite temperature quantum field theory.

The only quantities a black hole has are gravitational invariants, which are observables at infinity and the scalar curvature R. Functions of gravitational invariants are also gravitational invariants such as its volume, area, radius, etc.

Gravitational manifolds are metric spaces that have isometric symmetries, and these gravitational invariants are invariants under these symmetries. If the metric space is Minkowski space, the isometric symmetries are just the familiar Poincare group.

Black holes are stable objects with no maximum mass

The black hole pressures—P_S, the outward pressure keeping it inflated from the negative scalar curvature, and P_M the inward pressure from self-gravity trying to compress it—are gravitational invariants. In the proof that P_S = -P_M , it is shown that the equilibrium is also stable and a universal black hole constant emerges F = 3c⁴/4G = 9.077…x10⁴³ N.

All black holes have the same force constant F inflating them, independent of black hole mass. It is this new black hole universal constant that explains why black holes have no maximum mass.

There are two immediate consequences of this universal force constant:

(1) The largest pressure in the universe, P_universe, is a physical observable and calculable. The smallest black hole has the highest pressure in the universe. Using the previously mentioned estimated minimum 2.35 solar mass, one obtains P_universe = 1.5183…x 10³⁵ N/m². This is an incomprehensibly large value, so we can compare it to the estimated center pressure of Jupiter P_Jupiter = 650 x 10⁶ pounds/in² (NASA website—uses British units), giving P_universe/P_Jupiter = 3.3878…x10²², still beyond human comprehension.

(2) There exists an area law for black holes to coalesce, but it is not Hawking’s guess and has nothing whatever to do with entropy. In order for two coalescing black holes to form with pressures P₁ and P₂ in the volume, leaving a remnant with pressure P₃, it is required that P₁+P₂ > P₃, otherwise the remnant cannot exist. Since the pressures are P = F/area, with universal force constant F, this gives the actual black hole coalescing area law, involving reciprocal areas 1/A₁ + 1/A₂ > 1/A₃. The available gravitational wave data is consistent with this reciprocal coalescing area law. The existence of the universal black hole constant controls the coalescence of black holes.

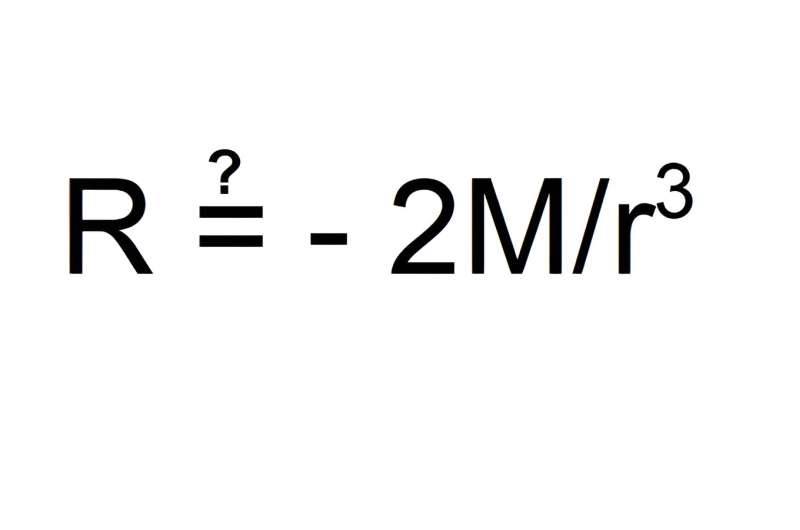
Question of black hole singularities

Applying causality to acausal spacelike matter always leads to contradictions. The widely quoted statement that black holes have a singularity is based on the misapplication of the causal Einstein equations of motion to acausal black holes, producing a fake singularity, see figure 2.

This equation is a contradiction, because the scalar curvature is a gravitational invariant on the left-hand side, but the right-hand side has spherical coordinates, which are not gravitationally invariant. In the article published in Reports in Advances of Physical Sciences, it is thus proved that black holes have no singularities.

Contradictions always arise if causal physics is applied to black hole spacelike matter

There are contradictions that arise if causal finite temperature quantum field theory is misappropriated to acausal spacelike black holes: In a commonly cited reference, Hawking did this exact misappropriation and stated that black holes have a temperature and evaporate away their mass, reaching the vacuum state.

Where is the contradiction that we expect when causal physics is applied to acausal spacelike black holes? If black holes truly radiated, their mass would indeed approach zero, but as Figure 1 shows, their negative scalar curvature R does not go to zero, but instead goes to negative infinity: The black hole end state is not the required vacuum state R = 0. This is the contradiction that arises from misappropriated causal finite temperature field theory to acausal spacelike matter.

Renormalization of the scalar curvature R

One of the goals in general relativity is the renormalization of R in four-dimensional spacetime. It is shown in a 2018 article that the renormalization of R in finite temperature quantum field theory satisfies the same theorem as the renormalization of the thermodynamic potential.

Both quantities are physical observables that have no “legs” (meaning no external Green functions) in Feynman diagrams. The “infamous” prediction in quantum field theory that the electroweak vacuum energy density is 10¹²⁰ orders of magnitude larger than the experimental vacuum energy density is a false statement, because this constant term cancels out in the renormalization theorem for the thermodynamic potential.

Finally, one can say that the planet Jupiter, because of causality, is inarguably a much more complicated object than an acausal black hole.

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about Science X Dialog and how to participate.

Dr. Peter Morley is a theoretical physicist. A partial listing of his papers can be found here: inspirehep.net/authors/996788